The Perfect Cube Factory

The Problem

Originally put forward by van Fraasan (1989), there are several versions, all essentially the same, of the Perfect Cube Factory.

The purpose was to demonstrate that the principle of indifference could give rise to contradictions and so was not a valid form of argument. Unfortunately for those putting it forward, the contradictions are due to an elementary arithmetic error of their own, and have nothing to do with indifference. Nonetheless, The Perfect Cube Factory has a certain historical interest.

This version, which I give because I consider it to be one of the clearer versions, is taken from Hájek (2012).

A factory produces cubes with side-length between 0 and 1 foot; what is the probability that a randomly chosen cube has side-length between 0 and 1/2 a foot? The tempting answer is 1/2, as we imagine a process of production that is uniformly distributed over side-length. But the question could have been given an equivalent restatement: A factory produces cubes with face-area between 0 and 1 square-feet; what is the probability that a randomly chosen cube has face-area between 0 and 1/4 square-feet? Now the tempting answer is 1/4, as we imagine a process of production that is uniformly distributed over face-area. This is already disastrous, as we cannot allow the same event to have two different probabilities (especially if this interpretation is to be admissible!). But there is worse to come, for the problem could have been restated equivalently again: A factory produces cubes with volume between 0 and 1 cubic feet; what is the probability that a randomly chosen cube has volume between 0 and 1/8 cubic-feet? Now the tempting answer is 1/8, as we imagine a process of production that is uniformly distributed over volume. And so on for all of the infinitely many equivalent reformulations of the problem (in terms of the fourth, fifth, … power of the length, and indeed in terms of every non-zero real-valued exponent of the length). What, then, is the probability of the event in question?

The paradox arises because the principle of indifference can be used in incompatible ways. We have no evidence that favors the side-length lying in the interval [0, 1/2] over its lying in [1/2, 1], or vice versa, so the principle requires us to give probability 1/2 to each. Unfortunately, we also have no evidence that favors the face-area lying in any of the four intervals [0, 1/4], [1/4, 1/2], [1/2, 3/4], and [3/4, 1] over any of the others, so we must give probability 1/4 to each. The event ‘the side-length lies in [0, 1/2]’, receives a different probability when merely redescribed. And so it goes, for all the other reformulations of the problem. We cannot meet any pair of these constraints simultaneously, let alone all of them.

The underlying logic

The argument is based on there being a contradiction. The precise description of that contradiction varies according to the way the author has described the problem, but the reason for its existence is always the same.

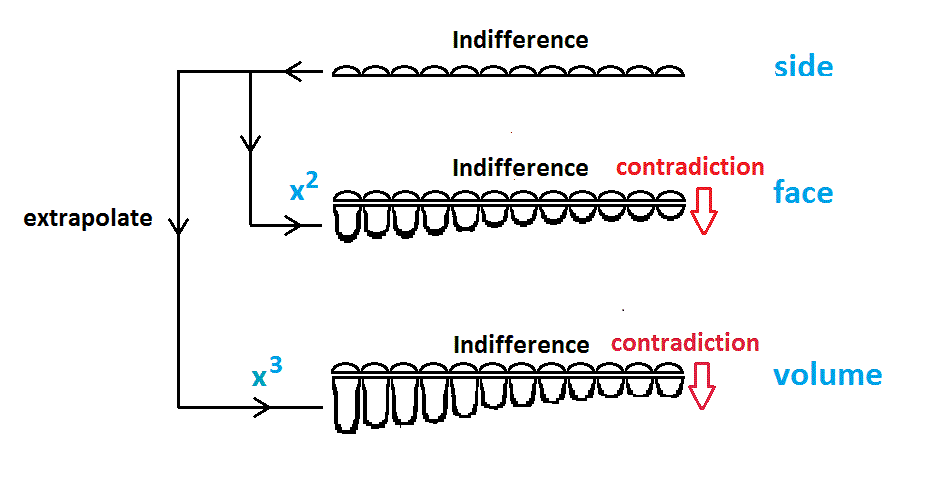
We seem to have two ways to calculate the distribution of face areas (Similar arguments apply to volumes). These are:-

1. To apply the Principle of Indifference directly to the distribution of areas, to obtain the uniform distribution.

2. To apply the Principle of Indifference to the distribution of side-lengths, so that they follow the uniform distribution, and then (because area=side²) extrapolate to the faces by squaring it. This gives the face-areas a non-uniform distribution.

(To do these, we need to subdivide the intervals of lengths/areas/volumes into smaller subintervals. That a cube might have its length, etc, falling into a subinterval is one of the "possibilities" referred to by Insufficiency. The diagram shows 12 such subintervals.)

So, the argument goes, there is a contradiction between the extrapolation and Indifference, and one (or both) of them must therefore be wrong. Since it cannot be (?) that the method of extrapolation is wrong -face areas are the square of sides- the error must be with Indifference.

As shown in the diagram, a similar contradiction is obtained when considering volumes.

What is going on?

A good place to start unravelling what is going on is with Hájek's question "What, then, is the probability of the event in question?". The answer to this is "We don't know: we would have to visit the factory and measure some cubes to know that."

Once we have answered that question, there follows another: "What, then, is the uniform distribution giving us?". The answer to this is that it is giving us an estimate -actually, the so-called best-estimate- of the distribution.

The uniform distribution of side-lengths is an estimate: an approximation which comes about because of a theoretical averaging process, usually making use of a symmetry argument. It is the mean over the set of all possible distributions. Likewise for the uniform distributions of face-areas or of cube-volumes.

So we have two different estimates of face-area, obtained in two different ways: one, by best-estimating them directly, the other by best-estimating the sides and then squaring that. Likewise for volumes (but involving cubing rather than squaring).

This is what is claimed to be the contradiction. However, there is nothing wrong with having two different estimates: there is no logical contradiction of the form  A & not-A, and having different estimates of the same thing is part of everyday science.

There is nothing contradictory or paradoxical about saying one estimate is uniform but the other is not uniform. The paradox arises only when we stop using the two different estimates as estimates and start treating them both as if they were the actual distribution: it is here that the contradiction arises, the distribution is uniform & the distribution is not uniform.

The Perfect Cube Factory goes wrong  by claiming that Indifference gives the actual probability rather than an estimate of, or mean of, the probability.