Often, there is no need to be
concerned about the value on the RHS, it being enough to note that if g
1,g
2 have the same degree and sample size then
LS(N)(g1)=LS(N)(g2).
This is not to say that the RHS is not important. It is actually very
important since it follows that
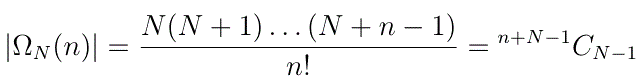
There is a geometrical way to obtain the same result.
The Combination Theorem is here named after the Combination Postulate, which was proposed by
William Ernest Johnson but not proved by him.
After trying for some time, Johnson eventually gave up relying on, or trying to
prove, this Postulate.
Johnson was a late 19th-early 20th century logician, based in Cambridge, working on probability theory and economics. His work is important in the history of the development of probability theory since it was linked to, and a close forerunner of, de Finetti's work on exchangeability.
At the time of his death in 1931, Johnson was working on a 4-volume work called
Logic, the first three volumes of which were published posthumously; the fourth volume was not completed.
In Volume 3 he wrote:-
... the calculus of
probability does not enable us to infer any
probability-value unless we have some
probabilities or
probability relations given.
The following two postulates in the Theory of
Eduction This is not a mistake. The word really is "Eduction"; it is not meant to be "Education". It means (http://www.thefreedictionary.com/eduction") "To infer or work out from given facts". are concerned with the possible occurrences of the determinates p
1
... p
n under the determinable P.
______
(1) Combination Postulate
In a total of M instances, any proportion, say m
1:m
2: ... :m
α
where m
1+m
2+...+m
α = M, is as likely as any other, prior to any knowledge of the occurrences in question.
(2) Permutation Postulate
Each of the different orders in which a given proportion m
1:m
2: ... :m
α for M instances may be presented is as likely as any other, whatever may have been the previously known orders.
______
In what follows certitude will be represented by unity.
By (1), the
probability of any one proportion
in M instances

I have here partitioned off the formal mathematical statements of his two postulates by horizontal lines. The paragraphs before and after them are informal commentary. I have also written the words
`probability' and `probabilities',
wherever they occur, in
red. I have done this to
emphasize that Johnson did not use the words 'probability' and 'probabilities' in the formal mathematics, only in the informal commentary.
Permutation Postulate
Any integram can be considered as an integram of observations, and those
observations -which would be made as a sequence of observations- could arise
in several orders. The integram (2,3), for example, could have arisen as the
sequence "1","1","2","2","2", or as the sequence "2","2","1","2","1", or as
the sequence, "2","2","2","1","1", etc. These are the
orders to which Johnson refers.
What Johnson is saying in the Permutation Postulate, is that we pay no
attention to the order in which observations are made, only to the final
total. The order in which the observations leading to (2,3) occurred is not
important, only the fact that the final histogram is (2,3).
There are exceptions to this (for example, if less weight is attached to
older observations), but generally speaking this is true for both
likelinesses generally -regardless of the underling set- or for specifically
probabilities -with singleton underlying sets.
Since the Permutation Postulate applies regardless of whether or not the
underlying set is singleton, Johnson would not have encountered any
difficulties by considering only probabilities - as he appears to have done
with the Combination Postulate.
This postulate is well-known as the introduction of the concept of
exchangability
Combination Postulate
Imagine rolling a die. In any one roll, there are six possibilities, or `determinates', namely "1", "2",
... , "6"; so α =6. If we were to roll the die 10 times then there would be 10 `instances' of those determinates; that is M=10. Say the number of rolls of each face were (1, 3, 0, 2, 2, 2) respectively: these are the values of the m
i. Of course, 1+3+0+2+2+2=10: that is, we have an ordered 6-tuple of non-negative integers summing to 10: this is an ordered 6-partition of 10.
What is confusing to the modern eye is Johnson's use of the word `proportion' to refer to something which we would not usually think of as a proportion. He is using it to refer to an ordered 6-tuple such as
(1, 3, 0, 2, 2, 2), ie. what we are here calling an integram. The Combination Postulate, when it says that any proportion is as likely as any other, is saying that any integram is as likely as any other of the same sample size.
There are two questions remaining about Johnson's wording, concerning the circumstances under which the
integrams are equally likely, and the meaning of the word `likely'.
- Johnson uses the expression ``prior to any knowledge of the occurences in question''. That knowledge can come from two places: theory and observation, so there must be no knowledge from either source. No knowledge from theory suggests that the underlying set should be S(N); no knowledge from observation suggests that the given histogram should be
0. So, for example, if we consider the tossing of a coin then all we know about the probability-pair (Pr(``H''),Pr(``T''))
is that it is --as all probability-pairs must be-- somewhere on the line
segment from (0,1) to (1,0)
- So far as the meaning of the word `likely' is concerned, there are two possible contenders: probability and best-estimate of probability, ie. likeliness. It has to be remembered that we are specifically maintaining the distinction between the two.
In the formal wording of the Combination Postulate, Johnson uses the word `likely' but does not actually refer to probabilities. He does use the word `probability', but only outside of that formal wording. This admits the possibility that, when drafting the formal wording, Johnson may have been thinking (albeit at an intuitive level) of a wider concept than `probability' but subsequently interpreted it as meaning specifically probability. Whether or not this was the case must, of course, be a matter of speculation but the condition he states does suggest that he may have been thinking about the expected value of the probability, ie. what happens on average, rather than the probability itself.
So could it be that Johnson's wording of the Combination Postulate was correct but that his stated interpretation of it in terms of probabilities, rather than expected values of probabilities, was not? This would certainly cause him difficulties, as we know happened.
The Combination Theorem answers this with "YES".
Combination Theorem
We start with a Lemma.
Theorem
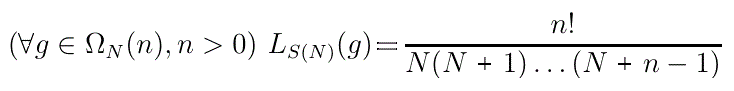
Proof
Given any g for which n=ω(g)>0, it is always possible to find an i for which g(i)>0. Since K
n is independent of that i we may use the Lemma as a reduction formula to repeatedly reduce the sample size in steps of 1 -without needing to worry about which i is being used at any step- until it reaches 0, at which point we have
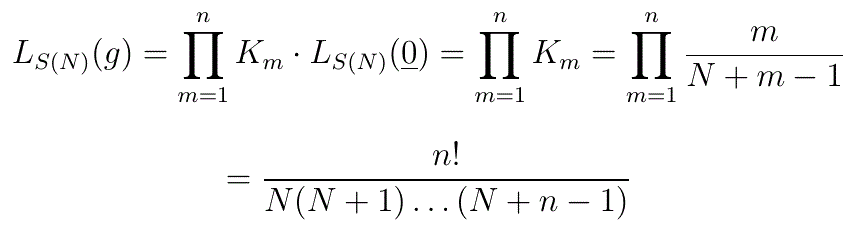

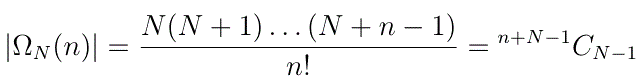

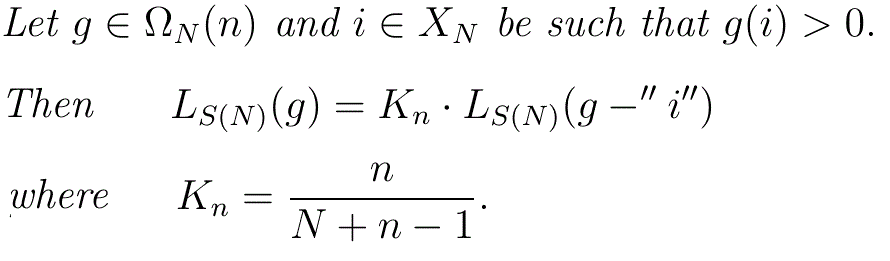
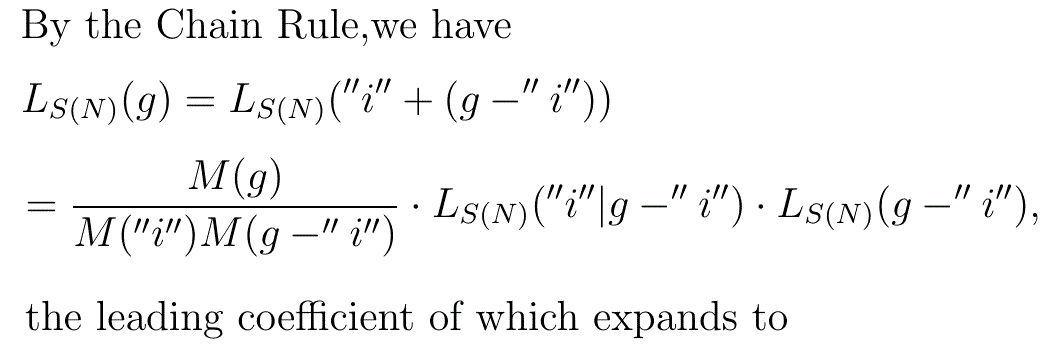
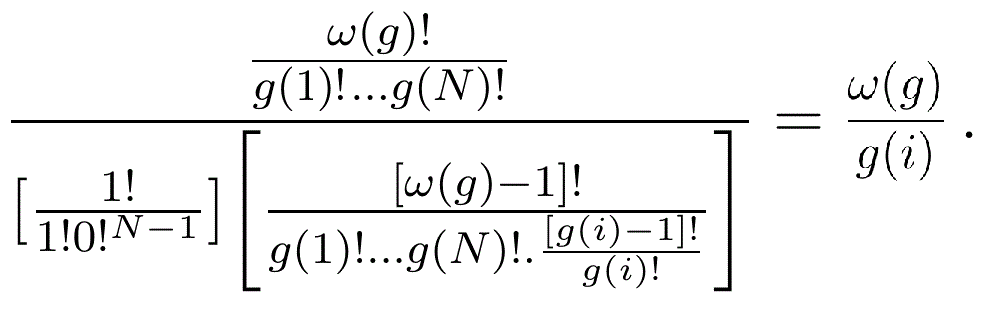
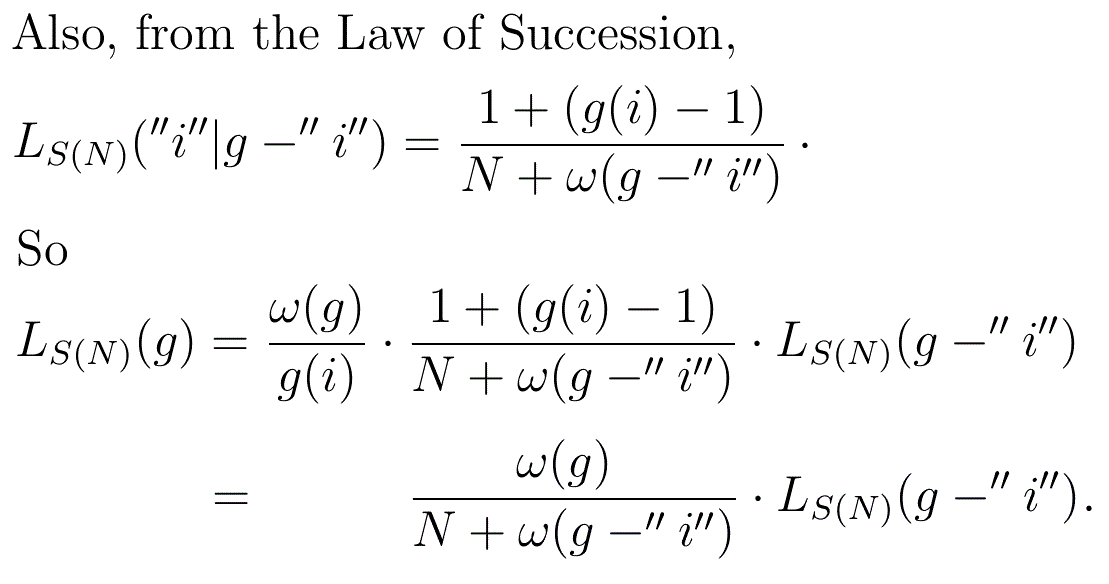
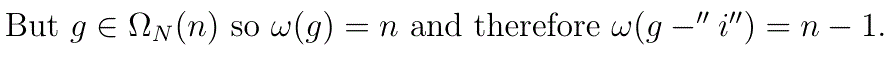
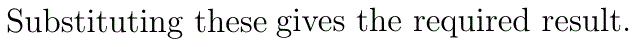
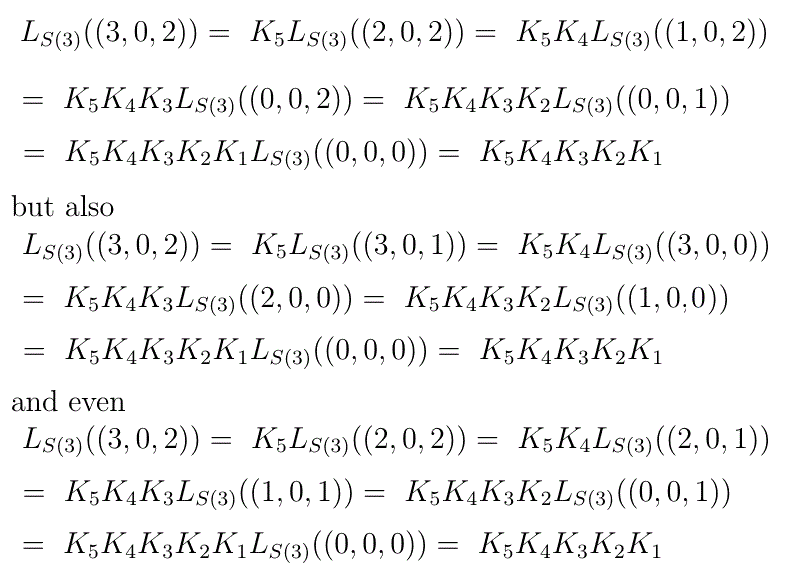
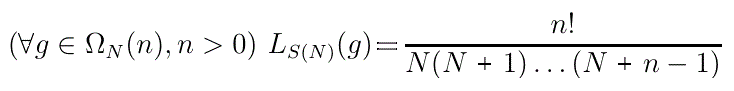
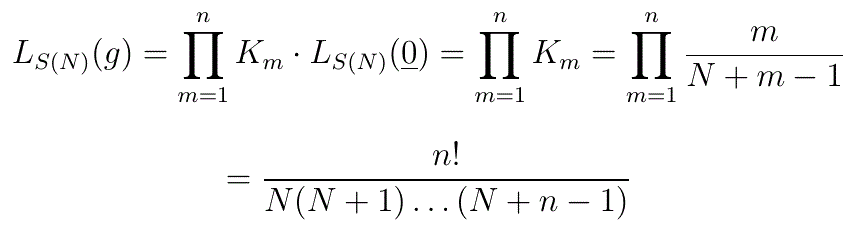
Using S(N) as the underlying set means that we have no theoretical reason for eliminating any distribution as a possibility. Having the zero histogram as the given histogram means that we have no information from observations.
This "know nothing" property makes the Combination Theorem very useful when we are trying to develop general principles.