Precision and Accuracy

• Precision is a measure of how spread out the values are.
• Accuracy is a measure of how close the values are on average to the correct value.

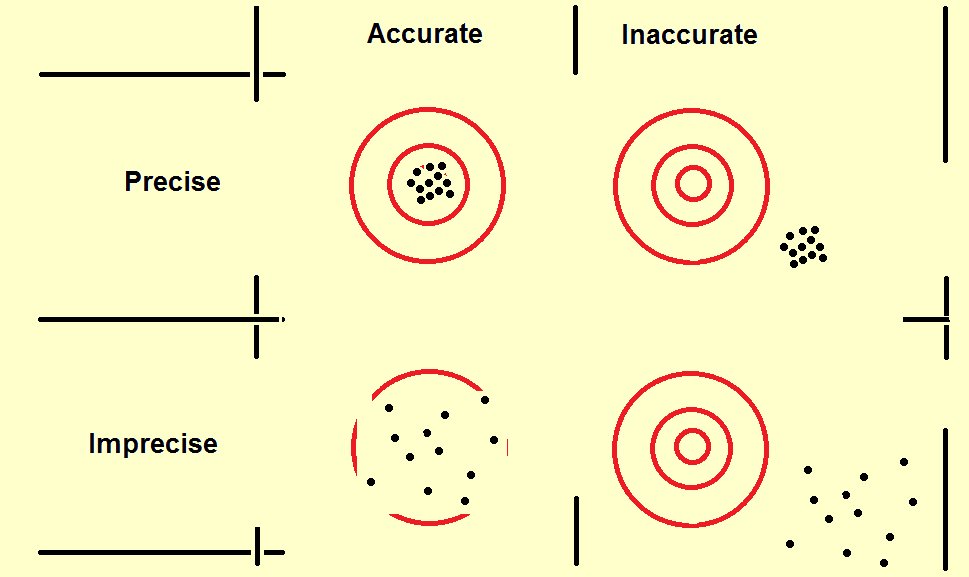
If the correct value is known, then inaccuracy is easily corrected by the addition of a constant vector. Correction of imprecision is much harder to carry out since it normally needs more widespread alterations and attention to detail. If the diagrams really were of shot-patterns then the inaccuracies could be easily corrected by adjusting the sights: this would take just a couple of tweaks with a screwdriver (remember the melon scene in The Day Of The Jackal). Improving the precision would mean having to control one's breathing; learning to squeeze the trigger rather than jerking it; holding the gun more firmly, etc. In other words, learning to be a better shot.

There is, though, one big BUT. We can measure precision since it depends upon just the known data. BUT we cannot usually measure accuracy since it depends upon knowing the correct value -and if we knew that then we presumably wouldn't be carrying out the analysis to begin with. In the diagrams, if the red target were removed then we could still see how spread out the shots were, but we would have no idea which, if any, were centred correctly. Are these shots accurate or inaccurate?Which of the two topmost diagrams did that come from?

It is possible to carry out simulations under mathematical conditions which match the real conditions as closely as possible -which is why Great Likelinesses produces sampling files. Although these can give a good indication of accuracy, they are rarely absolutely ideal because of modelling errors.