Sequential Distributions

Basic concept

Imagine an inclined ramp, down which some balls are rolled. At intervals, it is punctured by N holes through which the balls might fall. From the top of the ramp downwards, the holes are labelled 1, 2,..., N. Whenever a ball falls through hole i it is said to produce the output i .

Having reached a hole, a ball might fall through it or might get past it and travel down the ramp to the next hole. All balls reach the first hole. All the balls which reach the last hole fall through it (think of it as being the end of the ramp: everything that reaches it falls off the end). Each hole has at least one ball falling through it.

The proportion of balls reaching hole i will be denoted by F(i), and the proportion which produce the output i will be denoted by f(i). (To be clear, f(i) is the proportion of all balls; it is not the proportion of those reaching the hole. If 1000 balls are released, of which 350 reach hole 3 and 200 fall through the hole, then F(3)= 350/1000 and f(3)= 200/1000 (not 200/350) f is the sequential distribution.

General observations

1. f is the forward differences of F, that is f(i)=F(i)-F(i+1) with f(N)=F(N)
2. F is the cumulative sums from the right of f. For example, if N=3 then F(3)=f(3), F(2)=f(2)+f(3), F(1)=f(1)+f(2)+f(3)=1
3. 1=F(1)>F(2)>... >F(N)>0
4. Let r(i)= F(i)/[F(1)+...+F(N)], ie. r is the normalised form of F. Then r∈R(N)
5. F(i)=r(i)/r(1)

Bijection ψ_N:R(N)→S(N)

For each r∈R(N)

1. Divide r throughout by r(1) to give F:X_N→]0,1] with 1=F(1)>...>F(N)>0
2. Form f, the forward differences of F, f(i)=F(i)-F(i+1) with f(N)=F(N).

This process is invertible:-

For each f∈S(N)

1. Form F, the cumulative sums from the right of f;
2. Normalise F to give r∈R(N)

The importance of this bijection is that it gives meaning to the expression "choose a sequential system at random": choose r∈R(N) at random, and then find the corresponding (and unique) ψ_N(r).

Underlying set

The underlying set, SS(N), is the set of distributions produced by the algorithm.

Algorithm to produce f∈SS(N)

1. Select r∈R(N)
2. Divide throughout by r(1) to produce the function F(i)=r(i)/r(1)
3. Form the forward differences f(i)=F(i)-F(i+1) with f(N)=F(N).

Examples

Distribution of SS(3)

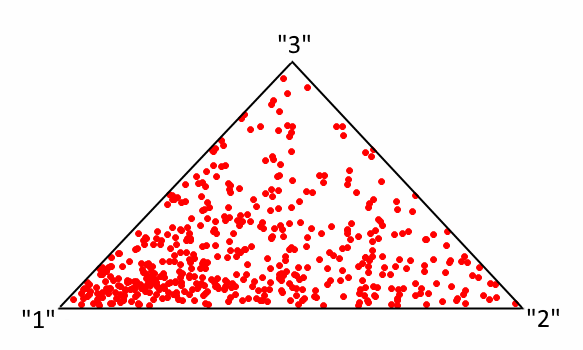
This Figure shows the distribution of 500 points in SS(3).