multinomial theorem

Prologue

Let P be a set of N strictly positive reals, say P={x₁, ..., x_N}.

If n is a non-negative integer then usually the mean of the n'th powers of x₁, ..., x_N is not equal to the n'th power of their mean. Sometimes, however, it is. Under what circumstances do we have equality?

The mean of the n'th powers is [x₁ⁿ+ ... +x_Nⁿ]/N
The n'th power of the mean is [(x₁+...+x_N)/N]ⁿ

It is not difficult to identify 3 cases:-

N= 1 We have x₁ⁿ/1 and [x₁/1]ⁿ, respectively
n= 0 We have N/N and (something)⁰, respectively
n= 1 We have [x₁+...x_N]/N in both cases

We can write these as:-

P is a singleton set: case (i)
n<2: cases (ii)&(iii)

Of these, 1 is the important case. 2 is trivial: we usually wouldn't even think about invoking the Multinomial Theorem to raise something to the power 0 or 1.

The relevance of this is that we are talking about the interaction between means and raising to powers. The importance of this is that we are inter alia talking about:-

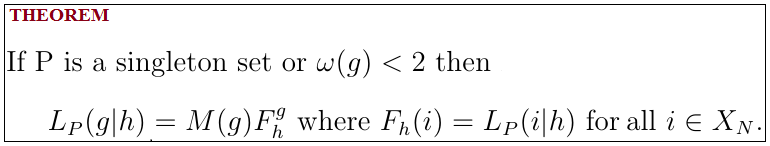
The interaction between likelinesses and the Multinomial Theorem.: Likelinesses are mean probabilities, and the Multinomial Theorem is all about raising to powers.
The Perfect Cube Factory.: The argument behind The Perfect Cube Factory is founded on the squaring (and cubing) of mean distributions and then comparing with the mean of squares.

Commentary on the Multinomial Theorem

The proof of the Theorem can be found in Fundamentals of Likelinesses.

The statement that 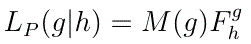is what I call the 'Multinomial Statement'.

The LHS of the Multinomial Statement is basically about the mean of powers, with the RHS being about powers of means. As would be expected from the Prologue, the Multinomial Theorem says that the Multinomial Statement applies if the underlying set is singleton or if the required integram is 0 or "i" (for some i).

Multinomial Consistency

'Great Likelinesses' calculates the Multinomial Consistency. This is the ratio between the two sides of the Multinomial Statement, and is given by .

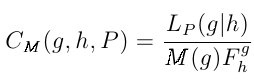This can be interpreted as the ratio between what we are trying to find -the best estimate of a probability- and what we get if we try to find it by substituting the best-estimates of the probabilities of "1", ...,"N" into the Multinomial Statement without regard to the conditions in the Multinomial Theorem.

Example

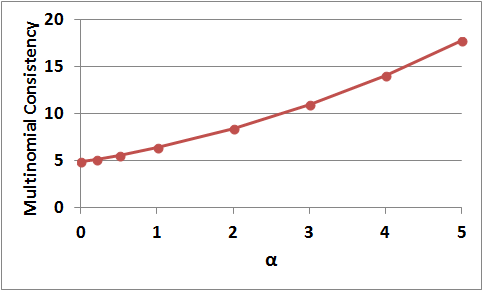
This figure shows C_M(g,αh,P) for g=(1,2,4), h=(1,0,0), P=R(3).

The introduction of α is a simple way of varying the sample size of the given histogram whilst keeping the relative frequencies the same.

This graph shows that if we were to best-estimate the probabilities of "1","2" and "3", and then treat those estimates as if they were the probabilities themselves (rather than just estimates) by substituting them into the Multinomial Statement then our estimate of the probability of (1,2,4) would be in error by a factor of about 5 with the given histogram h=(1,0,0), but that with h=(5,0,0) the error would be more than a factor of 15.

At heart, all that the Theorem is saying (or, rather, that its converse would say) is that -apart from a few simple exceptions, as stated in the Theorem- the mean of n'th powers isn't equal to the n'th power of the mean.

It is at this point that the Multinomial Theorem links with the Perfect Cube Factory.