Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
You should read the Research Report "Ranked Distributions on finite domains", available here, for full details of my research into ranked distributions.
Let f∈S(N) be such that [i<j]⇒[f(i)>f(j)].
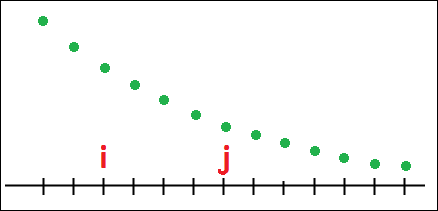
Then f is a ranked distribution. The set of all ranked distributions of degree N is denoted by R(N).
Let f∈S(N) be such that [i<j]⇒[f(i)<f(j)].
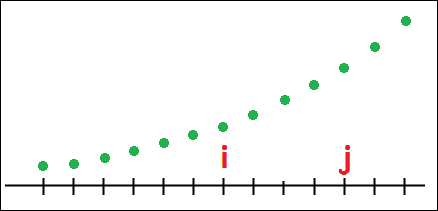
Then f is a reverse-ranked distribution.The set of all reverse-ranked distributions of degree N is denoted by RR(N).
The mapping defined by
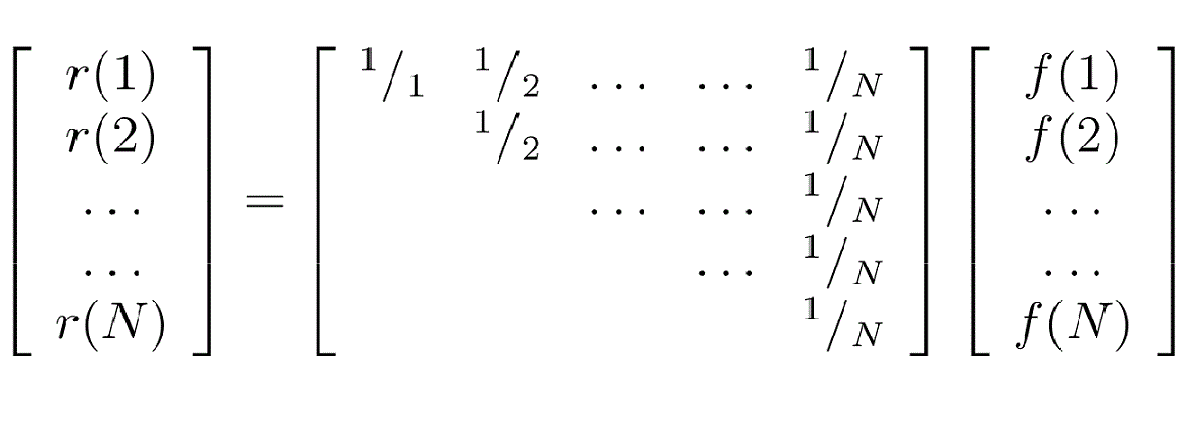
is a linear bijection from S(N) to R(N); for the proof, see "Ranked Distributions on finite domains". So, select f∈S(N) and then:-
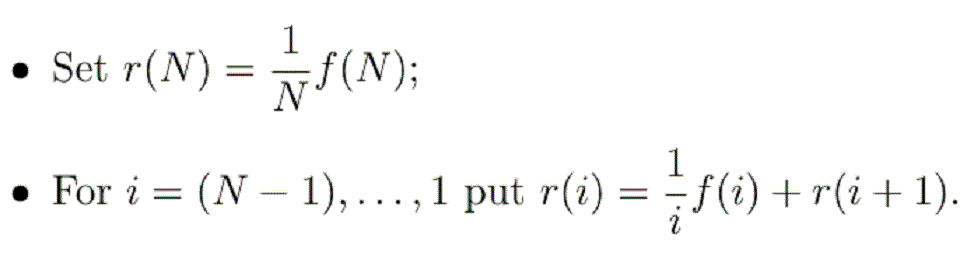
One way or another, this algorithm forms the basis for just about every (ie. except S(N)) algorithm on this site. Without this, none of the algorithms presented here could have been developed, and the calculation of non-trivial likelinesses would not have been possible.
The difference between ranked and reverse-ranked distributions is one of notation rather than intrinsic shape. Accordingly, reverse-ranked distributions, as entities in their own right, have no theoretical, and little practical, interest.
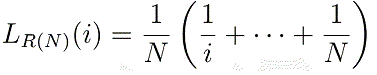
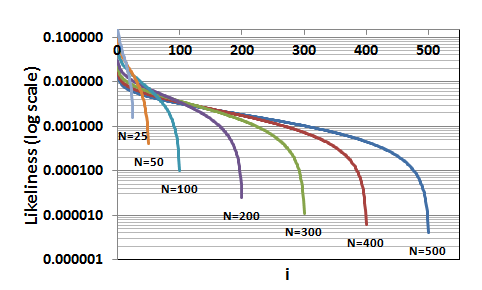
Graphs of this for various values of N are shown shown in the Figure.
This result places ranked likelinesses into a family of concepts centred around reciprocals of positive integers and, in particular, their means.
Other members of this family include:
Draw a table such as this one as a handout.
| Number of competitors | Favourite likely to win | Favourite not likely to win |
|---|---|---|
| 1 |
 |
|
| 2 |
 |
|
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 |
 |
To save time, announce that the favourite would be unlikely to win a competition between 20 competitors. Then get everyone to put a tick against each number of competitors to show whether or not they thought the favourite would be likely to win.
What they are looking for is that value of N for which LR(N)(1)>0.5 but LR(N+1)(1)<0.5. The ticks should all start off in the left-hand column and then swap over to the right. Where does the swap occur?
Try it for yourself, now, and then use the formula
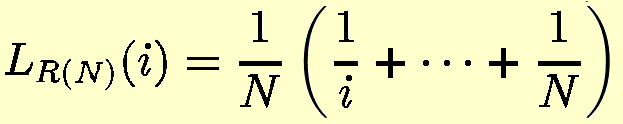
to see whether you're right.The answer is that N for which LR(N)(1)>0.5>LR(N+1)(1).
I've started the table off for you, so it's over to you. Any tick in the left-hand column must be preceeded by all ticks in the left-hand column. A tick in the right-hand column must be succeeded by all ticks in the right-hand column. What is the mathematical basis for this? So make life easy by going halfway and thinking about 10 competitors; this will allow you to fill in half of the table in one fell swoop.
Hover or tap here when you want to see the answer With four competitors the favourite is on average likely to win (likeliness=0.52), but not with five (likeliness=0.46). So the answer is N=4.